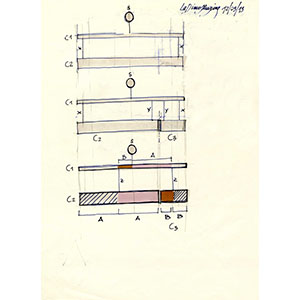
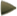Il principio della leva secondo Galileo
Posta all'inizio del secondo libro della Quadratura della Parabola di Archimede, questa dimostrazione sarà ripresa da Galileo. Il presupposto è l'equilibrio di un cilindro appeso nel suo punto centrale: una volta diviso in due parti diseguali, per avere equilibrio occorre che esse siano appese ai rispettivi centri. Nelle due posizioni, i pesi sono sostenuti una volta dai fili alle estremità, l'altra dai fili al centro. In quest'ultimo caso, i bracci da cui pendono sono inversamente proporzionali ai pesi dei due cilindri in equilibrio. Per questo le due parti sono collegate a un altro cilindro, a sua volta appeso al centro. Il principio che questo exhibit dimostra è che il sistema resta in equilibrio se sia gli spazi A e D che gli spazi B e C sono rispettivamente eguali. Infine, sostituendo i due segmenti di cilindro con oggetti di altra forma ma di peso equivalente, il sistema resta in equilibrio.